Ответ:
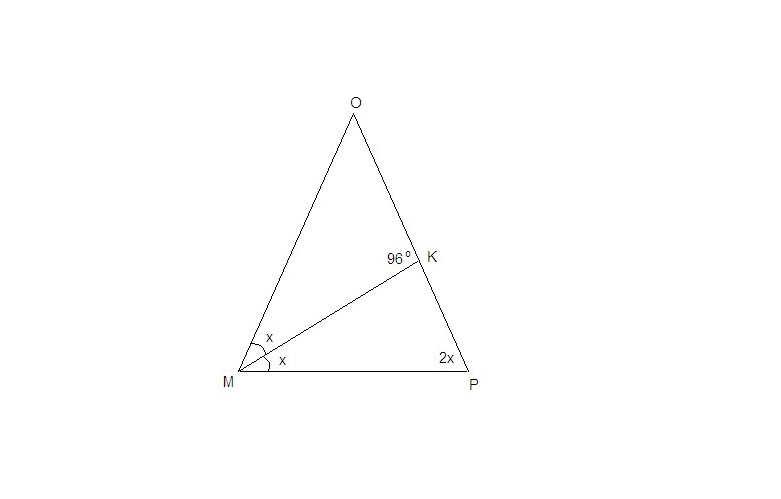
∠ОМК = ∠РМК = х (углы равны, так как МК — биссектриса)
Тогда ∠ОМР = 2х.
∠ОРМ = ∠ОМР = 2х как углы при основании равнобедренного треугольника.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
∠ОКМ — внешний для ΔМКР.
∠ОКМ = ∠КМР + ∠КРМ
x + 2x = 96°
3x = 96°
x = 32°
∠ОРМ = ∠ОМР = 2 · 32° = 64°